二阶贝塞尔曲线填充色 Quadratic bezier fill¶
Vertex shader¶
参数列表¶
参数类型 |
数据类型 |
变量名 |
说明 |
|---|---|---|---|
in |
|
|
从 manim 传入的顶点坐标 |
in |
|
|
单位法向量 |
in |
|
|
传入的颜色 |
in |
|
|
顶点索引 |
out |
|
|
贝塞尔曲线控制点 |
out |
|
|
传给 geom 单位法向量 |
out |
|
|
传给 geom 顶点颜色 |
out |
|
|
传给 geom 顶点索引 |
Geometry shader¶
几何图元¶
layout (triangle) in; // 输入图元
layout (triangle_strip, max_vertices=5) out; // 输出图元
参数列表¶
参数类型 |
数据类型 |
变量名 |
说明 |
|---|---|---|---|
uniform |
|
|
抗锯齿宽度 |
uniform |
|
|
帧大小 |
uniform |
|
|
焦距 |
uniform |
|
|
是否固定在画面上 |
uniform |
|
|
光源位置 |
uniform |
|
|
相机位置 |
uniform |
|
|
反光度 |
uniform |
|
|
光泽 |
uniform |
|
|
阴影 |
in |
|
|
贝塞尔控制点 |
in |
|
|
单位法向量 |
in |
|
|
颜色 |
in |
|
|
顶点索引 |
out |
|
|
颜色 |
out |
|
|
是否填充 |
out |
|
|
uv 坐标下的抗锯齿宽度 |
out |
|
|
xyz 坐标系 |
out |
|
|
方向 |
out |
|
|
uv 坐标系 |
out |
|
|
uv 坐标系下的点 b2 |
out |
|
|
曲线阶数 |
Fragment shader¶
参数列表¶
参数类型 |
数据类型 |
变量名 |
说明 |
|---|---|---|---|
in |
|
|
由 geom 传入颜色 |
in |
|
|
是否填充 |
in |
|
|
uv 坐标系下的抗锯齿宽度 |
in |
|
|
xyz 坐标系 |
in |
|
|
方向 |
in |
|
|
uv 坐标系 |
in |
|
|
uv 坐标系下的点 b2 坐标 |
in |
|
|
曲线阶数 |
out |
|
|
片段颜色 |
程序流程¶
注意
该部分为笔者的个人理解,若有不当之处,欢迎批评指正。
三角剖分¶
对于一个由贝塞尔曲线构成的 VMobject,首先需要根据其顶点进行剖分,将整个图形按照顶点分割成一系列三角形。 这一操作被称作 三角剖分,由 earcut 来完成,具体的原理可以查看 WallBreaker5th 的视频 刵 。
三角剖分完成之后,就可以对 VMobject 上色了。我们需要对这一系列三角以及一些弓形着色。
顶点着色器¶
顶点着色器从程序中获取顶点的位置、颜色、顶点索引、法向量,并向下一层传递。
几何着色器¶
几何着色器接收一个基本图形——点,以这个点为中心,创建基本图形。在此处,该着色器接收的是 triangles ,并将 triangle_strip 作为输出,其顶点数量最大值为 5.
Quadratic bezier fill 的几何着色器中的图元有三角形和五边形,而五边形是对三角形的边进行了抗锯齿的优化, 对于宏观的理解来说差别不是很大。
假设原先的三个控制点为
[p0, p1, p2],则五边形的控制点可以理解为[p0, p0 + dt, p1, p2 +dt, p2]
上面提到了三角剖分,而此处的图元大多为三角形或者五边形,这里引入 fill_all 变量,用于指定按照直接三角形绘制,
或者对贝塞尔曲线的控制点进行抗锯齿优化后,按照五边形绘制。当传入的顶点索引是相邻的正整数(例如 1, 2, 3 或 2, 3, 4 ),
那么就不使用直接三角形绘制。至于为什么这样做,下面解释其原因。
假设有一个圆,它由八段贝塞尔曲线拼接而成,每段由 3 个控制点构成。给这个圆上填充色之前,我们需要对它进行三角剖分, 分割为一些三角形和边上的八个弓形。这些图形被称为“图元”,它们都是由 3 个控制点构成的。
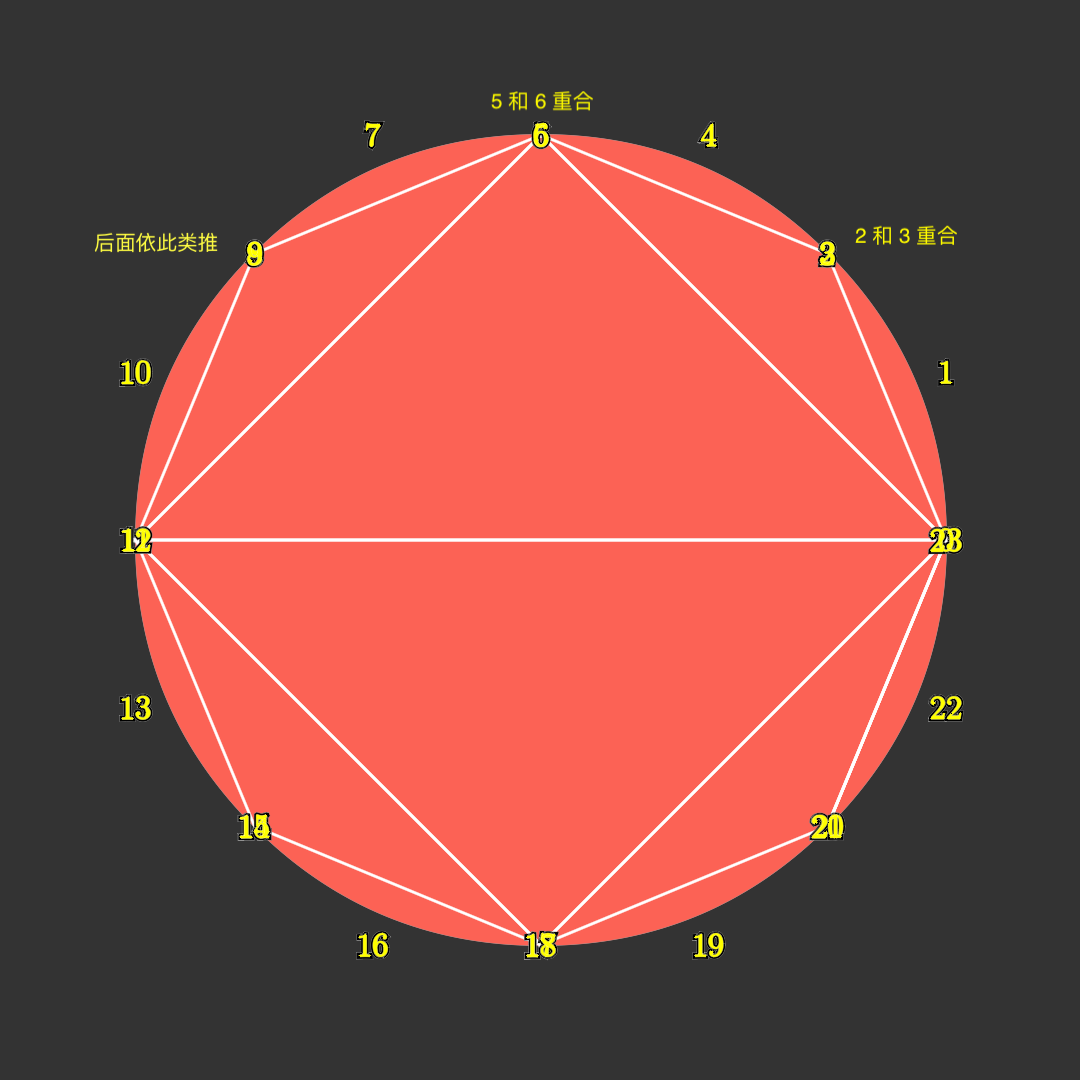
对于内部的这些三角形,注意到它们的三个顶点索引几乎都是不相邻的整数,我们可以直接采用直接三角形方案来上色。
而对于外面的这些弓形,它们的三个控制点索引几乎都是相邻的整数,因此我们不采用
fill_all的方案, 而是而采用贝塞尔曲线的上色方案。
接下来真正上色的工作就留给片段着色器。
片段着色器¶
在此模块开始前,建议先看一看 OpenGL 预备知识
对于内部的这些三角形图元,片段着色器只需无脑地把颜色传递给 frag_color 即可,因为这些三角形图元不涉及到较为复杂的曲线上色。
而对于边缘上的弓形,我们就需要使用 sdf 符号距离函数来进行一些处理。我们采用这样的方案:
由三个控制点构成的贝塞尔曲线的弓形,可以被这三个控制点所构成的三角形覆盖,因此我们可以先无脑地不管是什么样的图元, 我们都按照三角图元来上色,这样也就直接覆盖了上面的情况。

而边缘的弓形也被涂成了三角形,这与我们的目标有一些偏差。此时
fill_all参数的用途就得以体现了:当fill_all == 1.0说明此时是直接三角形绘制;否则,我们就按照贝塞尔曲线的上色方法,通过 sdf 计算,使得在弓形内部的像素点,保持其透明度不变; 而在弓形外部的像素点,其透明度为 0
另外,还有一些细节,例如指定向曲线凹陷处填充等等,在此不过多阐述。
此时, VMobject 的填充色着色程序工作完成。